缘由

这是一个早就想解决的问题，曾经做01背包的练习就是单纯地套用模板，近期看到一篇很好的文章，又有了新的一些体悟，特此记录。

状态函数及状态转移方程：

函数 $f(i,j)$ 表示考虑前 $i$ 个物品，设定总空间为 $j$ 时的最大价值。

$$w(i)>j \text{ 时, }f(i,j) = f(i-1,j)\text{ （放不下）}$$

$$w(i)<=j\text{ 时，}f(i,j) = max[f(i-1,j) ,f(i-1,j- w(i))+v(i)]$$

误区纠正：学习方法

之前学习算法（尤其是DP），总是觉得自己应该整体上“理解”这个算法，而忽略了从列表、特殊数据等方面来辅助学习的方法。其实，如果对01背包问题感到难以理解，多半是因为不愿意认真列表分析一个特例。

状态函数

函数 $f(i,j)$ 表示考虑前 $i$ 个物品，设定总空间为 $j$ 时的最大价值。

定义很清晰，但是理解时可能会不经意间进入下列误区：

• 对 $i$ 的理解，应当是考察了前 $i$ 个物品，并不是说这前 $i$ 个物品都进入了背包；
• 对 $j$ 的理解，是考察前 $i$ 个物品时，赋予的总空间，而不是所谓“剩余空间”；
• 所给空间 $j$ 并不一定要恰好填满，而是不能超过。

状态转移方程

• $w(i)$ 与 $j$ 比较大小时，考察的是“就算把空间全都给第 $i$ 件物品，它能不能放进去”，体现的是一种优先思想，即优先考虑第 $i$ 件物品。先决定它放不放进去，然后再说编号 $1…(i-1)$ 的物品如何处理。在这样的操作方法下，当第 $i$ 件物品是否放入背包已经确定时， $f(i,j)$ 最大的情况就等价于考察前 $i$ 件物品最大时的情况。

时空复杂度的优化

该部分参考了dd_engi大佬的背包九讲

原问题较为显然的实现应当是定义二维数组 $f[N][V]$ （其中 $N$ 为物品数， $V$ 为背包最大容量），然后以 $i=0…N$ 为外层循环， $j=0…V$ 为内层循环，“逐行填表”，最后输出 $f[N][V]$ 即可。这样写的话时间和空间复杂度均为 $O(NV)$ ，事实上，算法的复杂度还可以进一步地优化，其中空间复杂度优化最为显著。

先上一张图，便于下面进行描述。

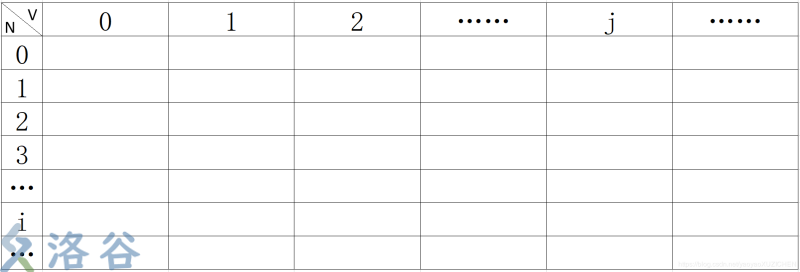
空间复杂度的优化

注意到，在外层循环进行到某个特定的 $i$ 时，进行内层循环时， $i$ 相对于变化的 $j$来讲暂时不变, $w[i]$ 自然也暂时不变。那么，若使 $j$ 从后往前扫描（即 $j=V,V-1,…,0$ ），则每次可能用到的 $f[i-1][j-w[i]]$ 的“正下方”那一格 $f[i][j-w[i]]$ 都暂时未被计算。

利用这一特性，不妨将数组减去一维，即将 $f[N][V]$ 简化为 $f[V]$ ，那么 $f[i-1][j-w[i]]$ 就相应地改写为 $f[j-w[i]]$ 。由于 $j$ 是从后向前遍历的，所以用到 $f[j-w[i]]$ 时，它的值还尚未被更新，实质上就相当于“上一行的” $f[i-1][j-w[i]]$ 。

时间复杂度的优化

上面应该注意到，公式的

$w(i)>j$ 时， $f(i,j) = f(i-1,j)$

这一条并没有体现出来。

事实上，当 $j<w[i]$ 时，由于 $f(i,j) = f(i-1,j)$ ， $f[j]$ 就根本没有必要更新。于是，只需令 $j=V…w[i]$ (而不是循环到 $j=0$ )，就可以使 $j=0,1,…,w[i]-1$ 都不更新，相当于是“把上一行的值抄了下来”。

变形：分组背包

与传统01背包不同之处在于每次决策是决定是否从一组中拿一个物品，以及拿哪个（每一组中的物品最多只能拿一件）。

解决方法：略作变形，在决定 $f[j]$ 的值的时候枚举一下正在考虑的这组中的所有物品，最终决定拿不拿/拿哪个。

总结

01背包可能是最经典、最简单的动态规划问题了。理解好这一模型的方法、思路、技巧，对后续动态规划的进一步学习应当有较大帮助。

Last modified on 2020-05-14